boundary_conditions.jl

Inlet and outlet boundary conditions are applied at the beginning and at the ending of each time step respectively (see solveModel). Inlet (outlet) condition is applied by setting flow (pressure) value at the first (last) vessel node. Inlet and outlet compatibility relations are defined to compute the remaining quantities: P, u, A, c, and Q, u, A, c respectively.

function setInletBC

Parameters:
t ::Float current time in seconds.
dt ::Float \(\Delta t\), current time step.
v ::Vessel vessel data structure.
h ::Heart heart data structure.
Functioning
The flow (pressure) at the first node of the vessel (Q[1]) can be set by several functions. This function is selected by BC_switch from h data structure. The inlet compatibility relations are handled by inletCompatibility. 

function setInletBC(t :: Float64, dt :: Float64,
                    v :: Vessel,  h  :: Heart)

	if h.BC_switch == 1
		v.Q[1] = sinHeaviside(t, h)

	elseif h.BC_switch == 2
		v.Q[1] = gauss(t, h)

	elseif h.BC_switch == 3
      	if h.inlet_type == "Q"
    			v.Q[1] = inputFromData(t, h)
      	else
    			v.P[1] = inputFromData(t, h)
      	end
	end

	inletCompatibility(dt, v, h)
end

heart_data.BC_switch = 1 sets a half sine flow waveform at the vessel inlet. Flow values at each time step are computed by the following function:

function sinHeaviside \(\rightarrow\) flow::Float

Parameters:
t ::Float current time in seconds.
h ::Heart heart data structure.
Functioning
The flow waveform is always bigger than the initial flow rate assigned at the initialisation step, i.e. initial_flow (\(Q_i\) in the picture). The sinusoid is multiplied by the desired maximum flow rate flow_amplitude (\(A_Q\)), and by the heaviside step function. This is done in order to ensure only a positive inlet flow. We want also the waveform to be different than zero for the entire length of the systole, defined by h.sys_T variable. This is done by setting the sin argument as \(\frac{2 \pi t}{T_s}\). In this way we can define a systolic impulse as narrow as wanted without worrying about the cardiac period which is completely unrelated.
Returns:
Q ::Float flow rate value at current time. 

function sinHeaviside(t :: Float64, h :: Heart)

	return h.flow_amplitude*(sin(2*pi*t/h.sys_T)*heaviside(-t+h.sys_T*0.5)) +
          h.initial_flow
end

function heaviside \(\rightarrow\) ::Float

Parameters:
n ::Float
Functioning
\[ H(n) = \begin{cases} 0 \quad \text{if } n < 0, \\ 1 \quad \text{if } n \geq 0. \end{cases} \]
Returns:
H ::Float either 1 or 0. 

function heaviside(n :: Float64)

	if n < 0.

		return 0.

	else

		return 1.

	end

end

heart_data.BC_switch = 2 sets a gaussian shaperd flow waveform at the vessel inlet. The bell shape has smoother transition at \(T_s\) than sinHeaviside. As a result, the numerical scheme produces less oscillations due to that discontinuity. Flow values at each time step are computed by the following function:

function gauss \(\rightarrow\) flow::Float

Parameters:
t ::Float current time in seconds.
h ::Heart heart data structure. 

function gauss(t :: Float64, h :: Heart)
Functioning
t_hat variable tells us how many cardiac cycles have already been simulated. This is calculated with div(a, b) which returns a/b, truncating to an integer. 
	t_hat = div(t,h.cardiac_T)

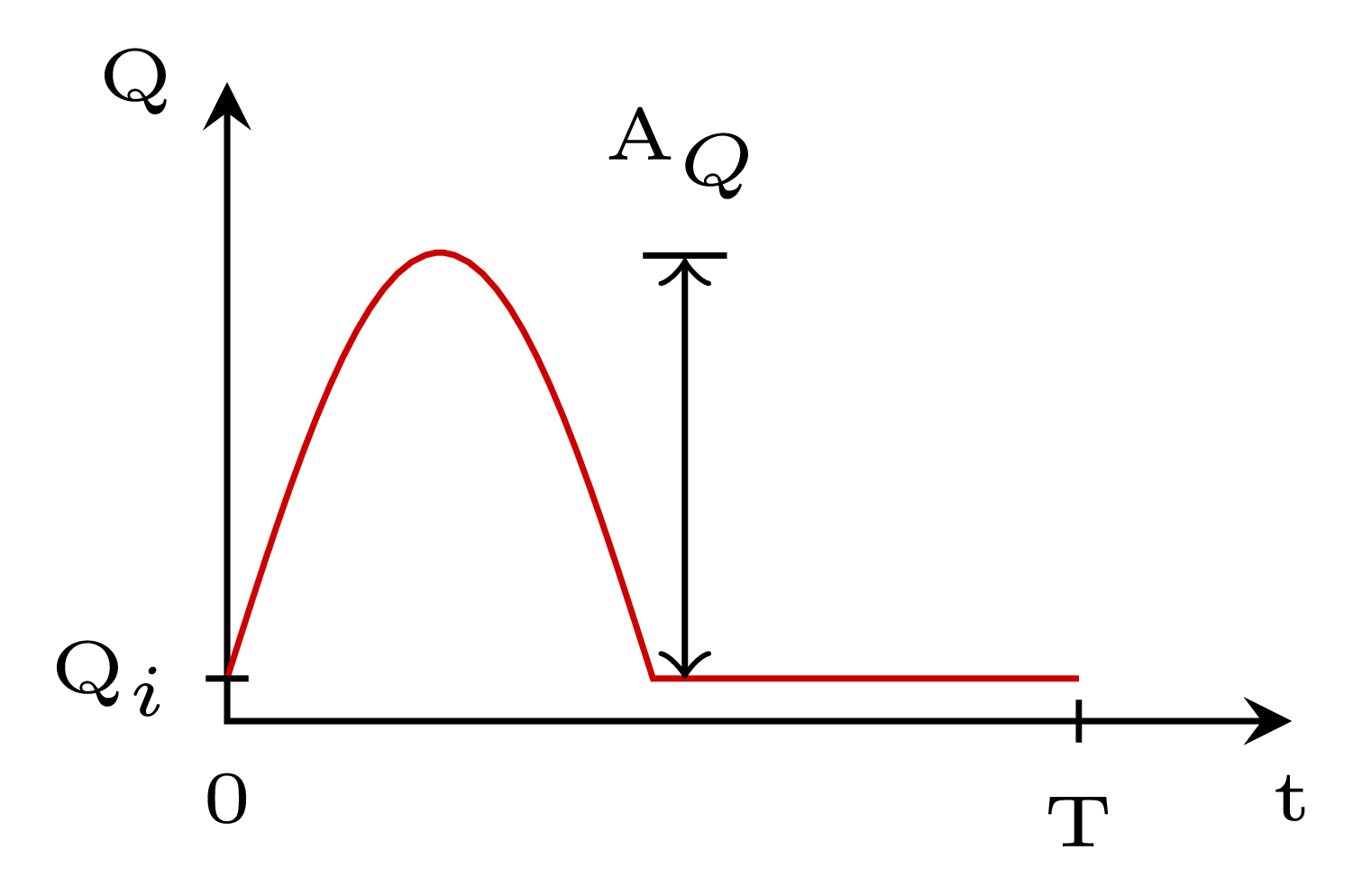
The gaussian bell should span the entire systolic period h.sys_T length. For gauss to return a value different than zero, the current time t must be within the current systolic period h.sys_T (\(T_s\)).

 
	if t < h.sys_T + h.cardiac_T*t_hat && t >= h.cardiac_T*t_hat

When this is confirmed, the inlet flow rate reads \[ Q = A_Q \exp{\left(- \frac{\left(t - \hat{t} T - \tfrac{T_s}{2}\right)^2}{2 \left(\tfrac{T_s}{8}\right)^2 }\right)} + Q_i. \] Variables are the same as those used in sinHeaviside.

 
		return h.flow_amplitude * exp( - (t-t_hat*h.cardiac_T -h.sys_T*0.5)^2 /
            (2*(h.sys_T*0.125)^2)) + initial_flow

Otherwise only the initial_flow is returned.

Returns:
Q ::Float inlet flow rate at current time. 
	else
		return 0. + initial_flow

	end
end

heart_data.BC_switch = 3 requires a flow waveform to be supplied by the user. The flow waveform is read by the following function:

function inputFromData \(\rightarrow\) flow::Float

Parameters:
t ::Float current time in seconds.
h ::Heart heart data structure. 

function inputFromData(t :: Float64, h :: Heart)
Functioning
Inlet flow waveform is stored in h data structure inside input_data matrix. input_data has two columns and as many rows as time steps. The first column (input_data[:,1]) contains the time variable. The second column (input_data[:,2]) contains the flow variable. The two arrays are copied into two variables, idt and idq respectively. 
	idt = h.input_data[:,1]
	idq = h.input_data[:,2]

t_hat variable tells us how many cardiac cycles have already been simulated. This is calculated with div(a, b) which returns a/b, truncating to an integer.

 
	t_hat = div(t,h.cardiac_T)

The current time is then updated by subtracting as many cardiac cycles as those already passed. This is done in order to have a reference within the cardiac cycle, i.e. in order to know at what point (when) in the cardiac cycle the simulation is running.

 
	t -= t_hat*h.cardiac_T

The waveform is given in a discrete form and usually with a small amount of points along the cardiac cycle. Usually, the numerical \(\Delta t\) is small enough to fall between two time steps reported in 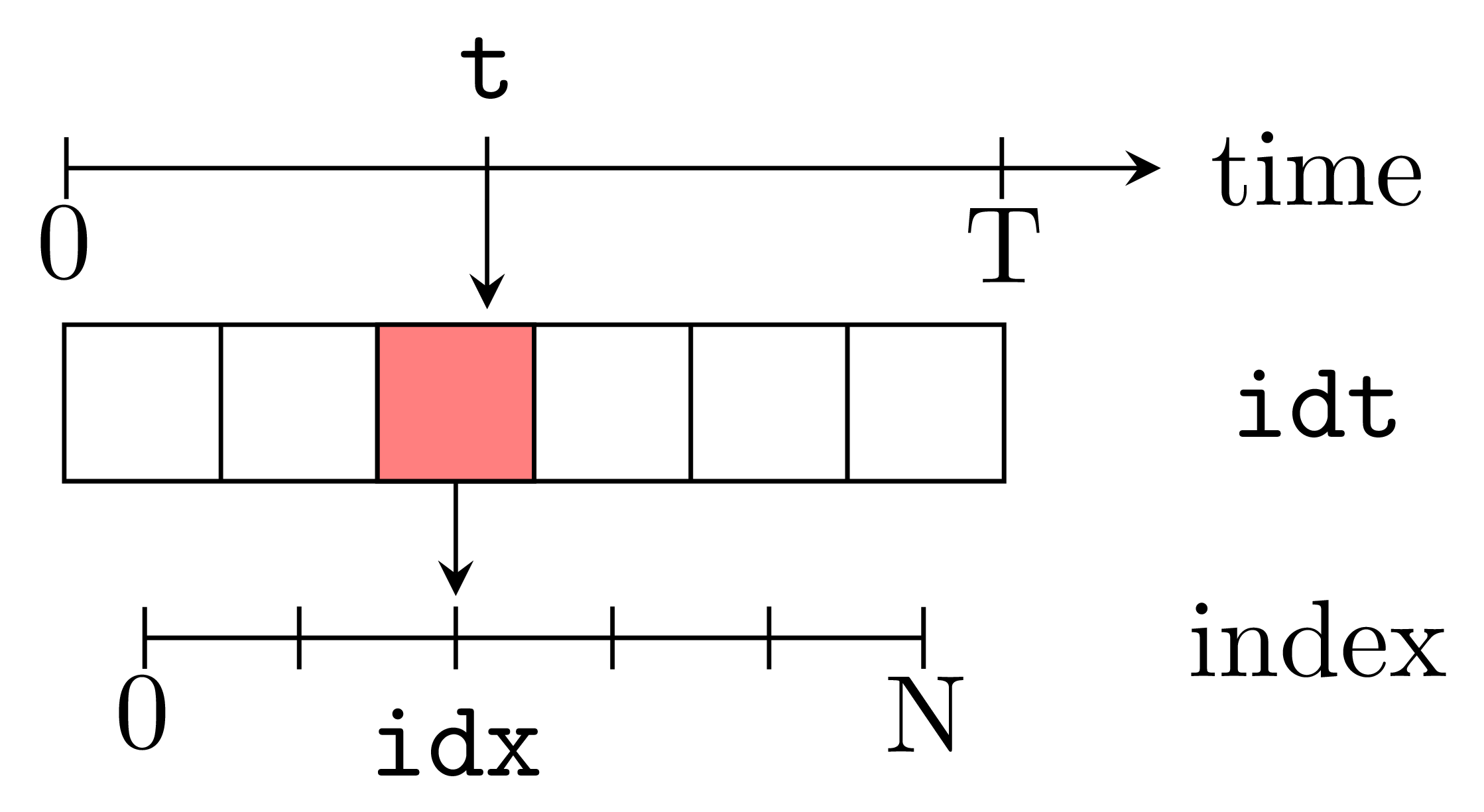idt. This loop skims all the entries in idt and finds the time interval containing the current time t. The variable idx is initialised to zero for simplicity.

 
	idx = 0
	for i in 1:length(idt)
		if ((t >= idt[i]) && (t <= idt[i+1]))
			idx=i
			break
		end
	end

The flow qu is then computed at the current time by a linear interpolation between the two known flows (idq[idx] and idq[idx+1]) at the ends of the time interval.

 
	qu = idq[idx] + (t - idt[idx]) * (idq[idx+1] - idq[idx]) /
       (idt[idx+1] - idt[idx])
Returns:
qu ::Float inlet flow rate at current time. 
	return qu
end

In the case of veins, the inlet is always coupled with three-element Windkessel. The inlet function is re-defined as follows

function setInletBC

Parameters:
v ::Vessel vein data structure.
dt ::Float \(\Delta t\), current time step.
Pc ::Float pressure across the peripheral compliance of the three-element Windkessel.
R2 ::Float peripeheral resistance of the coupled three-element Windkessel.
Functioning
The flow at the first node of the vein (Q[1]) is set as the flow exiting the three-element Windkessel computed as \[ Q_{vein-in} = \frac{P_c}{R_2}, \] and a small factor of 1e-10 is added to avoid numerical instabilities. Then, the inlet compatibility relations are computed. 
function setInletBC(v  :: Vessel,  dt :: Float64,
                    Pc :: Float64, R2 :: Float64)
	v.Q[1] = Pc/R2 + 1e-10

	inletCompatibility(dt, v)
end

The inlet compatibility relations are handled by inletCompatibility.

function inletCompatibility

Parameters:
dt ::Float \(\Delta t\), current time step.
v ::Vessel vessel data structure.
Functioning
Compatibility relations are derived by using a technique called extrapolation of characteristics 1. 

function inletCompatibility(dt :: Float64, v :: Vessel, h :: Heart)

Riemann invariants are computed starting from variables at time t. \[ W_{11}^t = u - 4c, \quad W_{21}^t = u + 4c, \] are computed at the inlet node of the vessel. W12 and W22 are the same quantities computed at the second node, i.e. the closest node at the right hand side of the inlet node.

 
	W11, W21 = riemannInvariants(1, v)
	W12, W22 = riemannInvariants(2, v)

The two Riemann invariants within the two nodes are extrapolated with a linear law. They reads \[ W_{11}^{t+1} = W_{11}^t + \left(W_{12}^t - W_{11}^t \right) (c_1 - u_1) \frac{\Delta t}{\Delta x}, \] \[ W_{21}^{t+1} = W_{21}^t - W_{11}^{t+1} + 2 \frac{Q_1}{A_1}, \] where the 1 subscript indicates the inlet node.

 
	W11 += (W12-W11)*(v.c[1] - v.u[1])*dt/v.dx
	W21 = 2*v.Q[1]/v.A[1] - W11

Longitudinal velocity and wave velocity at the inlet node are retrieved by rI2uc (Riemann invariants to u and c) function.

 
	v.u[1], v.c[1] = rI2uc(W11, W21)

A and P quantities follow from their definitions.

 
	if h.inlet_type == "Q"
		v.A[1] = v.Q[1]/v.u[1]
		v.P[1] = pressure(v.A[1], v.A0[1], v.beta[1], v.Pext)
	else
		v.A[1] = areaFromPressure(v.P[1], v.A0[1], v.beta[1], v.Pext)
		v.Q[1] = v.u[1]*v.A[1]
	end

end

function inletCompatibility(dt :: Float64, v :: Vessel)

	W11, W21 = riemannInvariants(1, v)
	W12, W22 = riemannInvariants(2, v)

	W11 += (W12-W11)*(v.c[1] - v.u[1])*dt/v.dx
	W21 = 2*v.Q[1]/v.A[1] - W11

	v.u[1], v.c[1] = rI2uc(W11, W21)

	v.A[1] = v.Q[1]/v.u[1]
	v.P[1] = pressure(v.A[1], v.A0[1], v.beta[1], v.Pext)

end

Outlet boundary condition is applied to the last node of the involved vessel. Two boundary conditions are available. Either a reflection coefficient is provided or a three elements windkessel is coupled.

function setOutletBC

Parameters:
dt ::Float \(\Delta t\), current time step.
v ::Vessel vessel data structure.
Functioning
Outlet boundary conditions are selected in the project.csv file. 

function setOutletBC(dt :: Float64, v :: Vessel)

A proximal resistance R1 set to zero means that a reflection coefficient was specified. Thus, the pressure P is first linearly extrapolated 2 as \[ P_M = 2 P_{M-1} - P_{M-2}, \] where \(M\) is the index of the vessel outlet node. Then, the compatibility relations are applied by means of outletCompatibility function.

 
	if v.R1 == 0.

		v.P[end] = 2*v.P[end-1] - v.P[end-2]
		outletCompatibility(dt, v)

When all the parameters of the three element windkessel are specified, wk3 function is called. This function solves lumped parameter equations and it also applies compatibility relations.

 
	else
		wk3(dt, v)

	end

end

Outlet compatibility relations compute all the quantities not directly assigned by the outlet boundary condition.

function outletCompatibility

Parameters:
dt ::Float \(\Delta t\), current time step.
v ::Vessel vessel data structure.
Functioning
Compatibility relations are derived by using a technique called extrapolation of characteristics as for the inlet. 

function outletCompatibility(dt :: Float64, v :: Vessel)

	W1M1, W2M1 = riemannInvariants(v.M-1, v)
	W1M, W2M   = riemannInvariants(v.M, v)

\[ W_{2M}^{t+1} = W_2^t + \frac{W_{2 M-1}^t - W_{2M}^t}{\Delta x} (u_M^t + c_M^t) \Delta t, \] \[ W_{1M}^{t+1} = W_{1M}^0 - R_t \left(W_{2L}^{t+1} - W_{2L}^0 \right). \]

 
	W2M += (W2M1 - W2M)*(v.u[end] + v.c[end])*dt/v.dx
	W1M = v.W1M0 - v.Rt * (W2M - v.W2M0)

Here the remaining quatities are computed by means of their definitions.

 
	v.u[end], v.c[end] = rI2uc(W1M, W2M)
	v.Q[end] = v.A[end]*v.u[end]

end

The three element windkessel simulates the perfusion of downstream vessels. This 0D model is coupled by 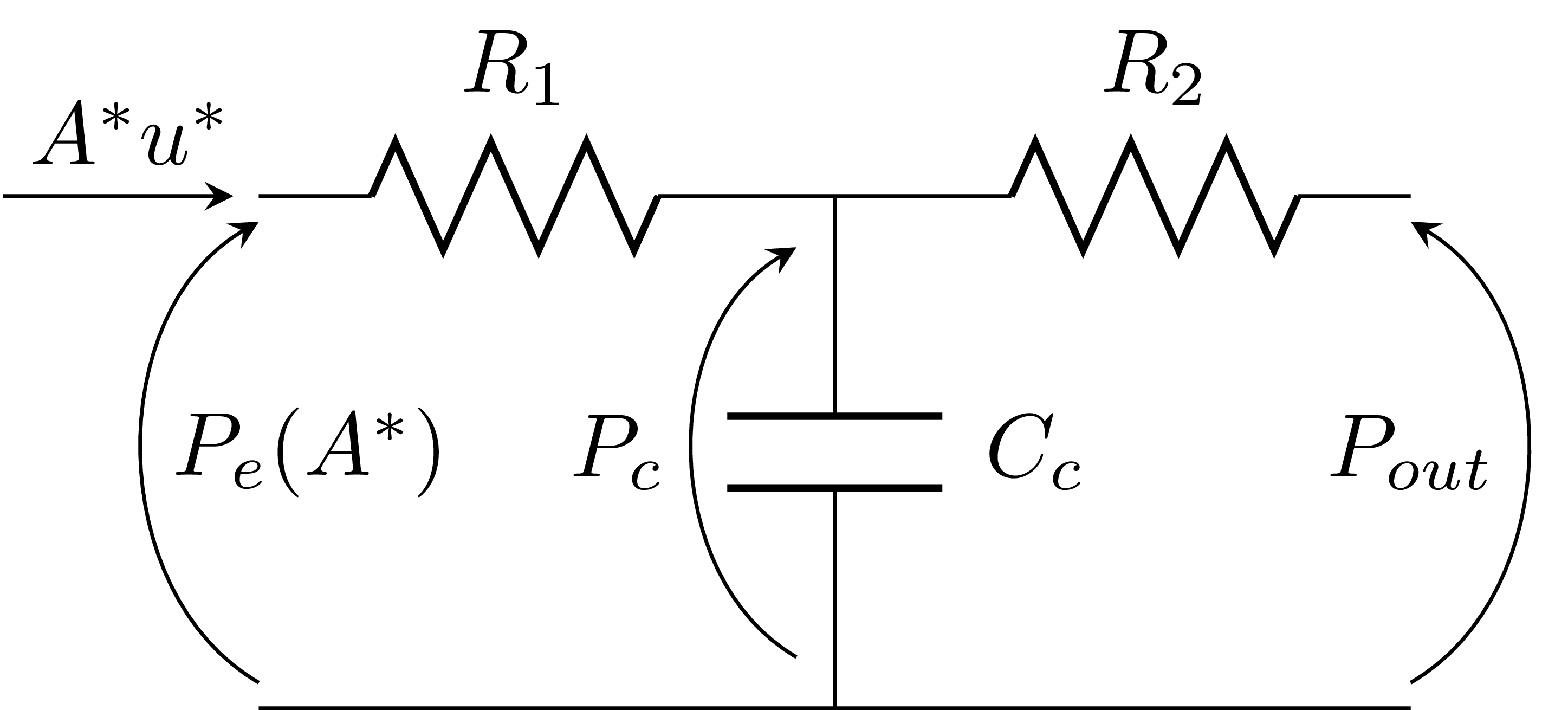wk3 function to 1D model terminal branches via the solution of a Riemann problem at the 0D/1D interface.

\(R_1\) is the proximal resistance, \(R_2\) is the peripeheral reisistance, \(C_c\) is the peripheral compliance, \(P_c\) is the pressure across the peripheral compliance, \(P_out\) is the pressure at the artery-vein interface, \(P_e\) is the pressure at the 0D/1D interface.

function wk3

Parameters:
dt ::Float \(\Delta t\), current time step.
v ::Vessel vessel data structure. 

function wk3(dt :: Float64, v :: Vessel)
Functioning 3
At capillary level the pressure is assumed to be zero, i.e. \(P_{out}=0.\) 
	Pout = 0.

The coupling is performed by assuming that an intermediate state \((A^*,u^*)\) generates from \((A_l,u_l)\) (1D outlet) and \((A_r,u_r)\) (0D inlet). This intermediate state must satisfy the windkessel equation \[ A^*u^* \left(1 + \frac{R_1}{R_2}\right) + C_c R_1 \frac{\partial (A^*u^*)}{\partial t} = \frac{P_e - P_{out}}{R_2} + C_c \frac{\partial P_e}{\partial t}. \]

 
	Al = v.A[end]
	ul = v.u[end]

\(P_c\) is computed at each time step from \[ C_c \frac{\partial P_c}{\partial t} = A^*u^* - \frac{P_c - P_{out}}{R_2}, \] which is discretised numerically with a first-order scheme. \(P_c\) is is initialised to zero.

 
	v.Pc += dt/v.Cc * (Al*ul - (v.Pc-Pout)/v.R2)

We consider \(\beta\) and \(A_0\) to be the same on both sides of the 0D/1D interface. It yields the nonlinear equation \[ \mathcal{F}(A^*) = A^*R_1\left(u_l+4c_l\right) -4A^*R_1c^* - \frac{\beta}{A_0}\left( \sqrt{A^*}-\sqrt{A_0}\right) + P_c = 0, \] where \(c_l\) and \(c^*\) are the wave speeds calculated with \(A_l\) and \(A^*\), respectively.

 
	As = Al

fun(As) = v.R1(ul+4sqrt(3v.gamma[end]sqrt(Al)0.5))As - 4v.R1sqrt(3v.gamma[end]sqrt(As)0.5)As - (v.Pext + v.beta[end]*(sqrt(As/v.A0[end]) - 1)) + v.Pc

dfun(As) = v.R1( ul +4sqrt(1.5v.gamma[end])(sqrt(sqrt(Al)) - 1.25sqrt(sqrt(As))) ) - v.beta[end]0.5/(sqrt(As*v.A0[end]))

 
	ssAl = sqrt(sqrt(Al))
	sgamma =  2*sqrt(6*v.gamma[end])
	sA0 = sqrt(v.A0[end])
	bA0 = v.beta[end]/sA0

	fun(As) = As*v.R1*(ul + sgamma * (ssAl - sqrt(sqrt(As)))) -
		(v.Pext + bA0*(sqrt(As) - sA0)) + v.Pc

	dfun(As) = v.R1*(ul + sgamma * (ssAl - 1.25*sqrt(sqrt(As)))) - bA0*0.5/sqrt(As)

\(\mathcal{F}(A^*)=0\) is solved for \(A^*\) with the Newton’s method implemented in Roots library. \(A^*\) is initialised equal to \(A_l\). As = newton(fun, dfun, As)

 
	As = newtone(fun, dfun, As)

Once \(A^*\) is found, \(u^*\) reads \[ u^* = \frac{P_e^* - P{out}}{A^*R_1}, \] where \(P_e^*\) is \(P_e\) calculated with \(A^*\).

 
	us = (pressure(As, v.A0[end], v.beta[end], v.Pext) - Pout)/(As*v.R1)

	v.A[end] = As
	v.u[end] = us

end

function newtone(f, df, x0)

	xn = x0 - f(x0)/df(x0)
	if abs(xn-x0)<= 1e-5
		return xn
	else
		newtone(f, df, xn)
	end
end

function updateGhostCells

Parameters:
v ::Vessel vessel data structure.
Functioning
Ghost cells are updated by assuming both ends as transmissive boundaries. 

function updateGhostCells(v :: Vessel)

	v.U00A = v.A[1]
	v.U00Q = v.Q[1]
	v.U01A = v.A[2]
	v.U01Q = v.Q[2]

	v.UM1A = v.A[v.M]
	v.UM1Q = v.Q[v.M]
	v.UM2A = v.A[v.M-1]
	v.UM2Q = v.Q[v.M-1]

end

updateGhostCells exploits julia’s multiple dispatch property. This function can handle one or more than one vessels organised in an Array structure.

 
function updateGhostCells(vessels :: Array{Vessel, 1})

	for vessel in vessels
		updateGhostCells(vessel)
	end

end

References

  1. Peiro, Joaquim, and Alessandro Veneziani. “Reduced models of the cardiovascular system .” In Cardiovascular mathematics, pp. 347-394. Springer Milan, 2009.↩

  2. Anderson, John David, and J. Wendt. Computational fluid dynamics. Vol. 206. New York: McGraw-Hill, 1995.↩

  3. Fernandez, Miguel Angel, Vuk Milisic, and Alfio Quarteroni. “Analysis of a geometrical multiscale blood flow model based on the coupling of ODEs and hyperbolic PDEs.” Multiscale Modeling & Simulation 4.1 (2005): 215-236.↩