conjunctions.jl

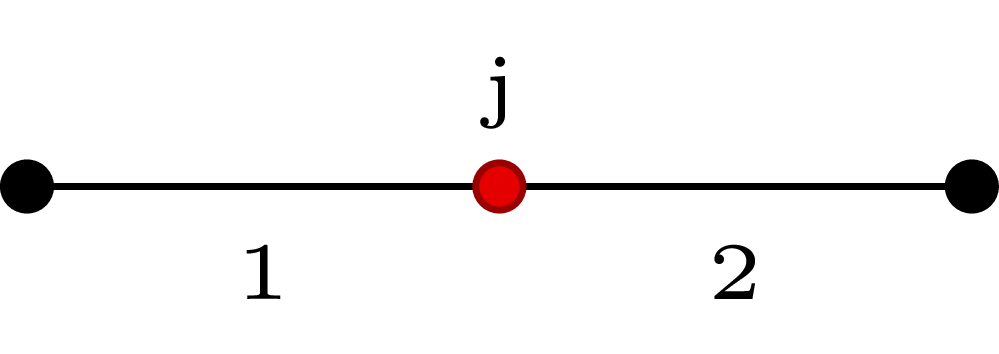
In a conjunction the left hand side vessel is called parent vessel and the right hand side vessel is called daughter vessel.

The conjunction is solved by imposing the conservation of mass and total pressure at the interface node \(j\). Two additional relations are obtained by extrapolating the outgoing characteristics from the two vessels. From parent vessel outlet we have \[ W_1 = u_1 + 4c_1, \] and for the daughter vessel inlet we have \[ W_2 = u_2 - 4c_2. \] The mass conservation reads \(A_1u_1 - A_2u_2 = 0\), and the total pressure conservation requires \(P_{t1} = P_{t2}\). By defining the unknown vector \(U\) as \[ U = \{U_i\} = \left\{ \begin{array}{c} u_1 \\ u_2 \\ A_1^{1/4} \\ A_2^{1/4} \end{array} \right\} , \quad i =1, ..., 4, \] the four relations read \[ F = \left\{f_i \right\} = \begin{cases} U_1 + 4k_1U_3 - W_1^* = 0, \\ U_2 - 4k_2U_4 - W_2^* = 0, \\ U_1U_3^4 - U_2U_4^4 = 0, \\ \beta_1 \left(\tfrac{U_3^2}{A_{01}^{1/2}} -1 \right) + \frac{1}{2}\rho U_1^2 - \beta_2 \left(\tfrac{U_4^2}{A_{02}^{1/2}} -1 \right) - \frac{1}{2}\rho U_2^2 = 0, \end{cases} \] where \(c_i = k_i A_i^{1/4}\), \(k_i = \sqrt{3/2 \gamma_i}\). \(F(U)=0\) is solved iteratively with Newton’s method 1 \[ \begin{cases} J \cdot \delta U = - F(U), \\ U^{new} = U + \delta U, \end{cases} \] where \(J\) is the Jacobian \[ J = \left[ \begin{array}{cccc} 1 & 0 & 4k_1 & 0 \\ 0 & 1 & 0 & -4k_2 \\ U_3^4 & -U_4^4 & 4U_1 U_3^3 & -4 U_2 U_4^3 \\ \rho U_1 & -\rho U_2 & 2 \beta_1 U_3/A_{01}^{1/2} & -2\beta_2 U_4/A_{02}^{1/2} \end{array} \right]. \] The entire process is handled by solveConjunction function.

function solveConjunction

Parameters:
b ::Blood model matrix row.
v1 ::Vessel data structure for the parent vessel.
v2 ::Vessel data structure for the daughter vessel.
Functioning
Firstly, the unknown vector \(U\) and parameters vector \(k\) are initialised with data from parent and daughter vessels. 

function solveConjunction(b :: Blood, v1 :: Vessel, v2 :: Vessel)

  U = [v1.u[end],
       v2.u[ 1 ],
       sqrt(sqrt(v1.A[end])),
       sqrt(sqrt(v2.A[ 1 ]))]

  k1 = sqrt(0.5*3*v1.gamma[end])
  k2 = sqrt(0.5*3*v2.gamma[ 1 ])
  k  = [k1, k2]

Riemann invariants are initialised by calculateWstarConj, the Jacobian is calculated by calculateJacobianConj, and the \(F\) vector is calculated by calculateFofUconj, and

 
  W = calculateWstarConj(U, k)
  J = calculateJacobianConj(b, v1, v2, U, k)
  F = calculateFofUconj(b, v1, v2, U, k, W)

Newton-Raphson method iterates until a tolerance on the error is met. The tolerance is defined on \(U\) and \(F\).

 
  nr_toll_U = 1.e-5
  nr_toll_F = 1.e-5

At the beginning of each iteration, \(\delta U\) is calculated by means of LU decomposition by julia’s command \. \(U\) is updated with an iterative step of 0.01.

 
  while true
    dU = J\(-F)
    U_new = U + dU

In the case the solution diverges, \(F\) will contain nan elements. In this case openBF exits the simulation and returns an error.

 
    if any(isnan(dot(F,F)))
      println(F)
      break
    end

When all the elements in \(\delta U\) and \(F\) meet the set tolerances, the solver stops the iterative loop.

 
    u_ok = 0
    f_ok = 0
    for i in 1:length(dU)
      if abs(dU[i]) <= nr_toll_U || abs(F[i]) <= nr_toll_F
        u_ok += 1
        f_ok += 1
      end
    end

    if u_ok == length(dU) || f_ok == length(dU)
      U = U_new
      break

If tolerances are not met, new \(U\), \(W\), and \(F\) vectors are computed and a new iteration starts.

 
    else
      U = U_new
      W = calculateWstarConj(U, k)
      F = calculateFofUconj(b, v1, v2, U, k, W)
    end
  end

Once the solution is found, quantities at both sides of the interface are updated.

 
  v1.u[end] = U[1]
  v2.u[ 1 ] = U[2]

  v1.A[end] = U[3]*U[3]*U[3]*U[3]
  v1.Q[end] = v1.u[end]*v1.A[end]

  v2.A[ 1 ] = U[4]^4
  v2.Q[ 1 ] = v2.u[1]*v2.A[1]

  v1.P[end] = pressure(v1.A[end], v1.A0[end], v1.beta[end], v1.Pext)
  v2.P[ 1 ] = pressure(v2.A[ 1 ], v2.A0[ 1 ], v2.beta[ 1 ], v2.Pext)

  v1.c[end] = waveSpeed(v1.A[end], v1.gamma[end])
  v2.c[ 1 ] = waveSpeed(v2.A[ 1 ], v2.gamma[ 1 ])
end

function calculateWstarConj \(\rightarrow\) W::Array{Float, 1}

Parameters:
U ::Array junction unknown vector.
k ::Array junction parameters vector.
Functioning
Riemann invariants are computed starting from unknown and parameters vectors as \[ W_1 = u_1 + 4c_1, \quad W_2 = u_2 - 4c_2. \]
Returns:
W ::Array containing outgoing characteristics at both sides of the conjunction. 

function calculateWstarConj(U :: Array, k :: Array)

  W1 = U[1] + 4*k[1] * U[3]
  W2 = U[2] - 4*k[2] * U[4]

  return [W1, W2]
end

function calculateFofUconj \(\rightarrow\) F::Array

Parameters:
b ::Blood data structure.
v1 ::Vessel parent vessel data structure.
v2 ::Vessel daughter vessel data structure.
U ::Array junction unknown vector.
k ::Array junction parameters vector.
W ::Array outgoing characteristics array.
Functioning
\(F\) array is computed by imposing the conservation of mass and total pressure. \(F\) reads \[ F = \left\{f_i \right\} = \begin{cases} U_1 + 4k_1U_3 - W_1^* = 0, \\ U_2 - 4k_2U_4 - W_2^* = 0, \\ U_1U_3^4 - U_2U_4^4 = 0, \\ \beta_1 \left(\tfrac{U_3^2}{A_{01}^{1/2}} -1 \right) + \frac{1}{2}\rho U_1^2 - \beta_2 \left(\tfrac{U_4^2}{A_{02}^{1/2}} -1 \right) - \frac{1}{2}\rho U_2^2 = 0, \end{cases} \]

Static pressure conservation can be imposed by replacing f4 with

f4 = v1.beta*( U[3] ^2 /sqrt(v1.A0) - 1) -
   ( v2.beta*((U[4])^2 /sqrt(v2.A0) - 1) )
Returns:
F ::Array Newton’s method relations. 

function calculateFofUconj(b :: Blood, v1 :: Vessel, v2 :: Vessel,
                           U :: Array, k :: Array, W :: Array)

  f1 = U[1] + 4*k[1]*U[3] - W[1]

  f2 = U[2] - 4*k[2]*U[4] - W[2]

  f3 = U[1]*(U[3]*U[3]*U[3]*U[3]) - U[2]*(U[4]*U[4]*U[4]*U[4])

  f4 = 0.5*b.rho*U[1]*U[1] + v1.beta[end]*(U[3]*U[3]/sqrt(v1.A0[end]) - 1) -
     ( 0.5*b.rho*U[2]*U[2] + v2.beta[ 1 ]*(U[4]*U[4]/sqrt(v2.A0[ 1 ]) - 1) )

  return [f1, f2, f3, f4]
end

function calculateJacobianConj \(\rightarrow\) W::Array{Float, 1}

Parameters:
b ::Blood data structure.
v1 ::Vessel parent vessel data structure.
v2 ::Vessel daughter vessel data structure.
U ::Array junction unknown vector.
k ::Array junction parameters vector.
Functioning
The Jacobian is computed as \[ J = \left[ \begin{array}{cccc} 1 & 0 & 4k_1 & 0 \\ 0 & 1 & 0 & -4k_2 \\ U_3^4 & -U_4^4 & 4U_1 U_3^4 & -4 U_2 U_4^4 \\ \rho U_1 & -\rho U_2 & 2 \beta_1 U_3/A_{01}^{1/2} & -2\beta_2 U_4/A_{02}^{1/2} \end{array} \right]. \]

The conservation of static pressure is imposed by setting to zero elements \(J_{4,1}\) and \(J_{4,2}\).

Returns:
J ::Array{Float, 2} Jacobian matrix. 

function calculateJacobianConj(b :: Blood, v1 :: Vessel, v2 :: Vessel,
                               U :: Array, k :: Array)

  J = eye(4)

  J[1,3] =  4*k[1]
  J[2,4] = -4*k[2]

  J[3,1] =  U[3]*U[3]*U[3]*U[3]
  J[3,2] = -U[4]*U[4]*U[4]*U[4]
  J[3,3] =  4*U[1]*(U[3]*U[3]*U[3]^3)
  J[3,4] = -4*U[2]*(U[4]*U[4]*U[4]^3)

  J[4,3] =  2*v1.beta[end]*U[3]/sqrt(v1.A0[end])
  J[4,4] = -2*v2.beta[ 1 ]*U[4]/sqrt(v2.A0[ 1 ])

  J[4,1] =  b.rho*U[1]
  J[4,2] = -b.rho*U[2]

  return J
end

References

  1. Press, William H. Numerical recipes 3rd edition: The art of scientific computing. Cambridge university press, 2007.↩